Bloom Filter
Author: @Alan Huang Date: Nov 19, 2020 Tags: 延伸閱讀 性質: Tech Share
為什麼這個主題值得分享
- 與日常生活息息相關,但我們卻不知道它(問題 or 資料結構本身)的存在
- 有效率的解決了一個困難的問題
- 現在剛好在學資料結構
情境
- 抖音有上億個使用者和上億則短片,為什麼抖音從來不會出現重複的影片?
- 當我們在創建 ig 帳號的時候,我們輸入 username,ig 不到一秒就可以告訴我們這個 username 有沒有被使用過。但 ig 有上億個 username,他怎麼這麼快確定的?
解決方法
考慮情境 1. ,不過我們使用 ig 當例子。
建表處理
每個 user 建一個 List,儲存已經看過的短片 id。
時間
- 確認一則 → O(log(n))
圖資料庫
每個 user 一個 node,每個短片一個 node。
graph database
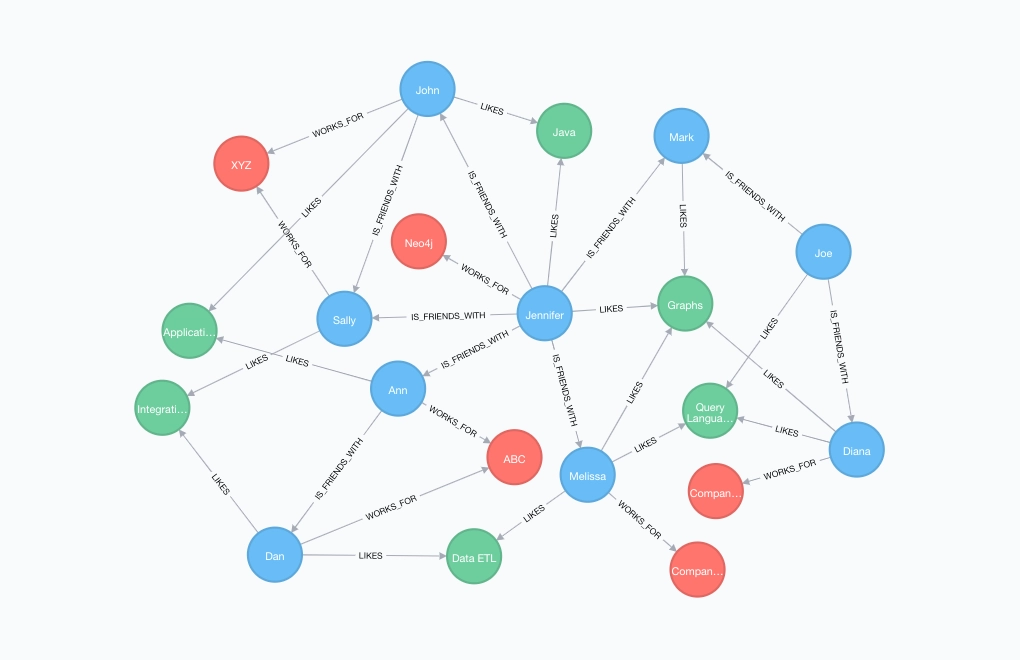
時間
我也不知道怎麼算,但總之 > O(1)。
Bloom filter
每個 user 一個 hash 表,儲存 0 / 1。
時間
- O(1)
Bloom Filter
有點類似集合,常用於快速檢查一個元素是否「可能存在」或「絕對不存在」於容器中。即會出現假陽性,但不會有假陰性。
優點
- 類似集合,可在 O(1) 時間複雜度驗證成員是否存在,卻僅需相對少的儲存空間。
- 承上,在 0.1% 錯誤率下儲存一百萬個元素僅需 1.71 MiB。
- 非常容易實作的機率資料結構,僅需多次雜湊。
缺點
- 原版 Bloom filter 容器大小固定(fixed-size),無法動態調整儲存空間(可透過變形解決)。
- 可能給出假陽性答案:回報存在但實際不存在,且錯誤隨數量變多上升。
- 自身不儲存成員資料,需要有額外的儲存資料方案。
- 只能新增成員,但不能移除成員(可透過變形解決)。
組成元素
- m 位元的位元陣列
- k 個 hash function
操作
插入
給定一個 key,利用 k 個 hash function 計算出 k 個 hash 值,將陣列中的 k 個位置設為 true。
查詢
給定一個 key,利用 k 個 hash function 計算出 k 個 hash 值,檢查 k 個位置,若皆為 true,則 key 存在。
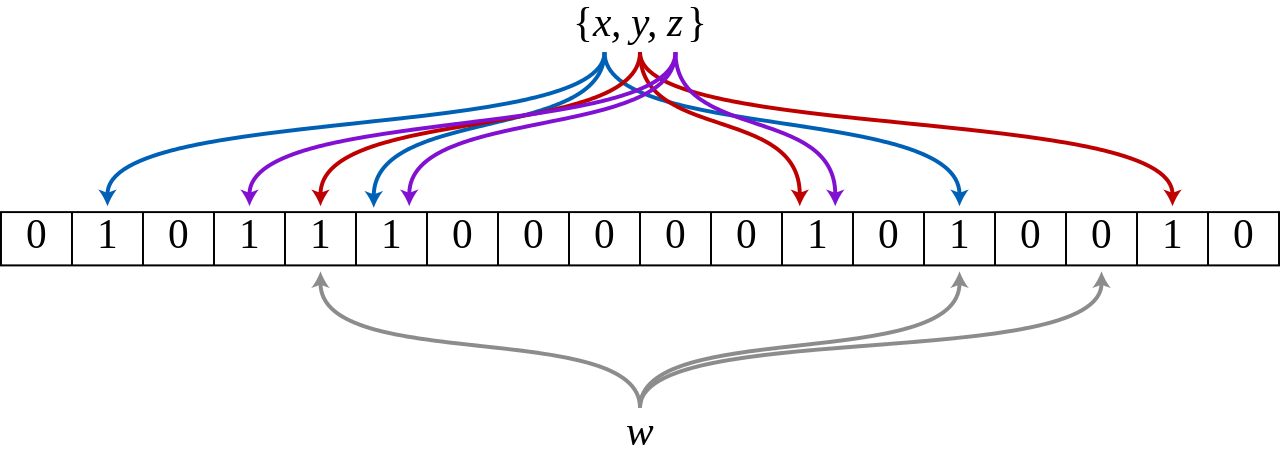
上圖顯示 w 並沒有在 {x,y,z} 集合中,因為 w 的雜湊結果有個位元為 0
問題
為什麼不直接使用 hash table(k=1)就好?
使用多個 hash function 以減少碰撞發生。
誤判的機率是多少?可以調整嗎?
回答這些問題需要兩個已知條件:
- 預期會儲存 n 個元素到容器。
- 可容忍的假陽性機率 ϵ。(即容器不包含該元素,檢測卻回報存在)
於是可得位元陣列最佳化的長度為 m 個位元,m 為:
$$m = -\frac{nln(\epsilon)}{(ln2)^2}$$
而在已知條件下,需要的雜湊函數數量 k 為:
$$k = - \frac{ln(\epsilon)}{ln(2)} = - log_2(\epsilon)$$
需要多個不同的 hash function?
double hashing → hash open addressing
這篇「Less Hashing, Same Performance:Building a Better Bloom Filter」提及,在不犧牲漸進假陽性機率(asymptotic false positive probability)的前提下,透過兩個不同的雜湊函數 $h_1(x)$ 和 $h_2(x)$,配合以下公式,就可以模擬出多個雜湊函數:
$$g_i = h_1(x) + ih_2(x)$$
hash → 給定 x (h(x) → key), O(1) 找到對應的 value
x → h(x) → hash table[h(x)] = y
使用情況
能允許假陽性(False Positive)的情況發生。
What is 假陽性 / 假陰性?
Confusion matrix
- 真陽性(True Positive)
- 真陰性(True Negative)
- 假陽性(False Positive)
- 假陰性(False Negative)
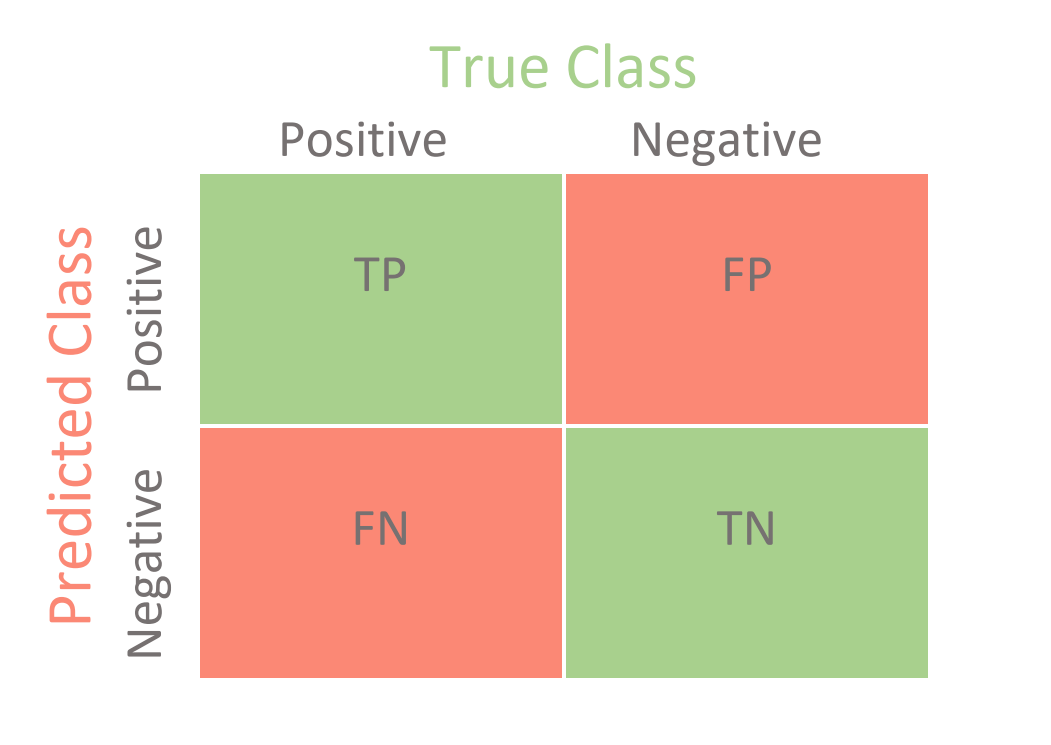
Example
- 避免推薦已看過的影片、文章
- 驗證大量惡意連結
變形
動態適應空間大小的 Scalable Bloom Filter
特色:動態適應空間大小,不需事先知道預期儲存的元素個數。
組成:由一至多個經典款 Bloom filter 組成。
插入:
若一個 filter 快滿了(超過 fill ratio),則會新增一個更大的 filter,往後所有新增都在這個新 filter 上面,直到它也滿了就再新增一個。
查詢:
Scalable Bloom Filter 比較弱的地方,查詢會從第一個 filter 開始找,若找不到往下一個 filter 找,找到會沒有下一個 filter 為止。若 filter 數量為 $l$,則查詢的時間複雜度從 $O(k)$ 變成 $O(k*l)$。
延伸 Topic
Reference
Great Source & 延伸閱讀
Topic 啟發點